Basic Linear Algebra
A quick introduction to the basic linear algebra needed in machine learning.
Mathematical Objects
Scalar
Single Number. \(\begin{align} S = 24 \end{align}\)
Vector
\[Vector: V = \begin{bmatrix}X_{1} \\ X_{2} \\ X_{3} \\ \end{bmatrix}\]Matrix
\(Matrix: u = \begin{bmatrix} u_{1} & u_{2} & u_{3} & ... & u_{4} \\ u_{1} & u_{2} & u_{3} & ... & u_{4} \\ . & . & . & . & . \\ u_{1} & u_{2} & u_{3} & ... & u_{4} \\ \end{bmatrix}\)
Tensor
3 axis. Row, column, depth.
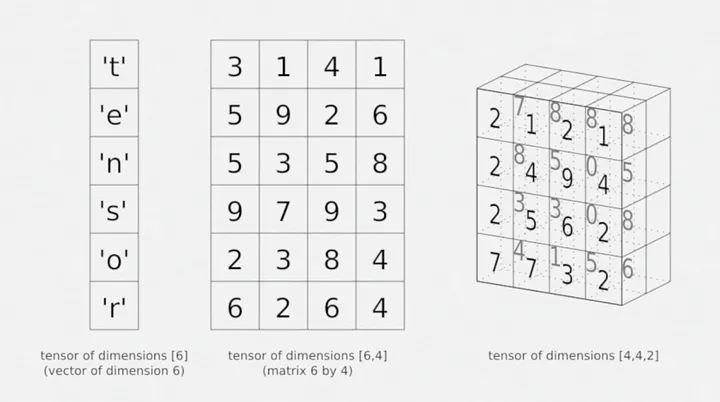
T232 = 0 Second column, third row, depth two.
A Tensor can be a Vector or a Matrix.
First-Order Tensor is a Vector. Second-Order Tensor is a Matrix. Third-Order Tensor and higher are called ‘Higher-Order’ Tensors.
Computational Rules
Matrix-Scalar Operations
Apply the scalar operation to every element of the matrix. \[\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} * y = \begin{bmatrix} a * y & b * y \\ c * y & d * y \\ \end{bmatrix}\]
Matrix-Vector Multiplication
\(\begin{bmatrix} a & b \\ c & d \\ e & f \\ \end{bmatrix} * \begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} a * x + b * y \\ c * x + d * y \\ e * x + f * y \\ \end{bmatrix}\)
Matrix-Matrix Addition and Subtraction
Matrices must have the same dimensions and the resulting matrix has the same dimensions.
Add or subtract the corresponding value of the first matrix with its corresponding value in the second matrix. \[\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} + \begin{bmatrix} e & f \\ g & h \\ \end{bmatrix} = \begin{bmatrix} a + e & b + f \\ c + g & d + h \\ \end{bmatrix}\]
Matrix-Matrix Multiplication
The number of the columns of the first matrix must correspond to the number of row’s of the second matrix.
The result of Matrix-Matrix multiplication will feature the number of columns of the first matrix and the number of rows of the second matrix.
To multiply two matrices split the second matrix into vector and multiply the first matrix buy each vectors separately then merge the resulting matrices into one without any operations between them. \[\begin{aligned} & \begin{bmatrix} 1 & 2 & 3 \\ 4 & 3 & 6 \\ \end{bmatrix} * \begin{bmatrix} 4 & 5 \\ 7 & 2 \\ 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} 27 & 12 \\ 55 & 32 \\ \end{bmatrix} \\ \\ & \begin{bmatrix} 1 & 2 & 3 \\ 4 & 3 & 6 \\ \end{bmatrix} * \begin{bmatrix} 4 \\ 7 \\ 3 \\ \end{bmatrix} = \begin{bmatrix} 27 \\ 55 \\ \end{bmatrix} \\ \\ & \begin{bmatrix} 1 & 2 & 3 \\ 4 & 3 & 6 \\ \end{bmatrix} * \begin{bmatrix} 5 \\ 2 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 12 \\ 32 \\ \end{bmatrix} \end{aligned}\]
Matrix Multiplication Properties
Not Commutative
Scalar multiplication is commutative but Matrix multiplication is not. \[\begin{aligned} Scalar: A*B = B*A \\ \\ Matrix: A*B \neq B*A \end{aligned}\]
Associative
Scalar and Matrix multiplication are both associative. \[\begin{aligned} Scalar/Matrix: A(B*C) = (A*B)C \end{aligned}\]
Distributive
Scalar and Matrix multiplication are both distributive. \[Scalar/Matrix: A(B+C)=A*B+A*C\]
Identity Matrix
The number 1 is an Identity because anything multiplied by one is equal to itself. A Matrix multiplied by an Identity matrix is equal to itself.
An Identity Matrix is recognizable by the fact that it is a “squared matrix” where its diagonal is equal to one and every other value is zero. \[\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \hspace{1cm} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \hspace{1cm} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\]
Multiplication by an Identity Matrix is the only exception where Matrix multiplication is commutative. \[\begin{bmatrix} 12 & 4 \\ 5 & 2 \\ \end{bmatrix} * \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} * \begin{bmatrix} 12 & 4 \\ 5 & 2 \\ \end{bmatrix}\]
Inverse and Transpose
Inverse
A number multiplied by its inverse is equal to one (Identity).
A Matrix multiplied by its inverse is equal to its Identity Matrix.
The only matrices to have inverses are “square matrices” but not every square matrix has an inverse.
We cannot divide Matrices. That is why multiplying by an inverse is useful because it results essentially in the same thing. \[\begin{bmatrix} 5 & 3 \\ 2 & 1 \\ \end{bmatrix} * \begin{bmatrix} \frac{2}{5} & -\frac{1}{5} \\ -\frac{1}{10} & \frac{3}{10} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\]
Transpose
A Transpose of a Matrix is a mirror image of the Matrix along a 45° axis.
Rows of the Matrix become columns of the Transpose Matrix.
A Matrix of size n * m is transposed to a Transpose Matrix m * n. \[\begin{aligned} A= \begin{bmatrix} 3 & 5 & 7 \\ 4 & 2 & 1 \\ \end{bmatrix} \\ \\ A^T= \begin{bmatrix} 3 & 4 \\ 5 & 2 \\ 7 & 1 \\ \end{bmatrix} \end{aligned}\]
